Psicometria (4/27): Partizione della varianza

Nel caso in cui si ha una variabile dipendente Y e due variabili indipendenti Y₁ e Y₂, con aree di varianza in condivisione (3 cerchi d'insieme tutti con una porzione condivisa tra di loro, X^Y₁^Y₂), esistono diversi coefficienti di correlazione:

Il coefficiente di correlazione semi-parziale (sr_y1.2) rappresenta la correlazione tra X₁ e Y quando X₂ viene parzializzata solo da X₁, e la sua formula è:




Il coefficiente di correlazione parziale (pr_y12) rappresenta la correlazione tra X₁ e Y quando X₂ viene parzializzata da X₁ e da Y, e la sua formula è:



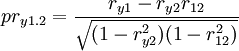
Il coefficiente di regressione (b_y1.2) rappresenta l'inclinazione della retta di regressione di Y su X₁ per valori costanti di X₂, cioè il cambiamento atteso in Y dopo un cambiamento di un'unità (nel caso di quello non standardizzato) o di una deviazione standard (nel caso dello standardizzato) in X₁ al netto di X₂.

Quindi, coefficiente di regressione non standardizzato:



Coefficiente di regressione standardizzato:



Le correlazioni parziale e semiparziale elevate al quadrato, misurano la quantità di varianza spiegata da una variabile indipendente, dopo che è stato tolto il contributo dato dalle altre variabili indipendenti.

La correlazione parziale al quadrato si calcola: pr²_y1.2=a/(a+e)

La correlazione semiparziale al quadrato si calcola: sr²_y1.2=a/(a+c+b+e)

<< Lezione precedente - Prossima lezione >>

 

Torna all'elenco delle lezioni