Psicometria (21/27): L'analisi della varianza (ANOVA)

L'analisi della varianza (ANOVA) è una tecnica di analisi dei dati che consente di verificare ipotesi relative a differenze tra le medie di due o più popolazioni.
Questa tecnica può essere usata quando la variabile dipendente è su scala a intervalli o a rapporti equivalenti, e quando la variabile indipendente è almeno categoriale.
I modelli che prevedono una sola variabile indipendenti vengono definiti disegni a una via, quelli che ne prevedono 2 o più, disegni fattoriali, i modelli che prevedono una sola variabile dipendente definiscono un'analisi della varianza univariata, quelli che prevedono 2 o più variabili dipendenti definiscono un'analisi della varianza multivariata (manova).

Analisi della varianza univariata
Ad ogni trattamento corrisponde un diverso gruppo di soggetti, ed in ogni condizione ci sono soggetti diversi: un soggetto esposto ad una condizione non viene esposto a nessun'altra, e questo metodo si estende anche per le variabili indipendenti.

Modello teorico dell'ANOVA
In questo modello tra i soggetti, il punteggio y_ij di un soggetto j nel gruppo i è scomponibile nel seguente modo:

y_ij=µ+a_i+e_ij

Dove:
µ è la media generale dei punteggi sul campione totale
a_i è l'effetto dovuto al trattamento, costante all'interno del trattamento
e_ij è una componente residua (o di errore casuale) specifica di ogni soggetto, che dipende da le differenze individuali tra i soggetti, l'errore di specificazione del modello, l'inattendibilità delle misure.
Il modello generale dell'ANOVA riguarda i dati della popolazione e per poterlo esaminare occorre definire le stime campionarie dei parametri di popolazione:
µ^=y^- è la media generale del campione
a^_i=(y^-_i-y^-) è la differenza tra la media dei gruppi e la media generale del campione che riflette il contributo della condizione i al punteggio del soggetto j
e^_ij=(y_ij-y^-_i) è la differenza tra il punteggio del soggetto e la media del gruppo in cui è inserito, e riflette la variabilità dei punteggi individuali all'interno di ogni gruppo.
Il punteggio di ij è esprimibile con la seguente formula:
y_ij=y^-+(y^-_i-y^-)+(y_ij-y^-_i)

Scomposizione della devianza totale
La devianza è la somma dei quadrati degli scostamenti tra ogni punteggio e la media.
In questo metodo, tutti i soggetti possono essere considerati come appartenenti ad un unico campione, e si possono quindi calcolare la media del campione complessivo e gli scarti tra i singoli punteggi e la media generale, dove la somma dei quadrati di questi scarti corrisponde alla devianza totale (SS_T).
Ogni gruppo sottoposto ad un diverso trattamento avrà una sua media, e si può annullare la variabilità all'interno di ogni gruppo, sostituendo al punteggio di ogni soggetto la media del gruppo e calcolare lo scarto tra i punteggi medi di gruppo e la media generale, dove la somma dei quadrati di questi scarti corrisponde alla devianza tra i gruppi, between (SS_B), cioè la variabilità tra i diversi gruppi.
Ogni punteggio dentro ogni gruppo si discosta dalla media del gruppo e la somma dei quadrati degli scarti tra i punteggi di ogni soggetto e la media di gruppo corrisponde alla devianza entro i gruppi, within (SS_W), cioè la variabilità dei soggetti all'interno di ogni gruppo.
La devianza totale SS_T può essere quindi scomposta in 2 parti: la parte dovuta alla deviazione delle medie di ogni gruppo dalla media generale (SS_B) e la parte dovuta alla deviazione dei punteggi dei soggetti dalla media del gruppo cui appartiene il soggetto (SS_W).

Gradi di libertà e quadrati medi
Per ciascuna delle 3 componenti della variabilità si può definire un opportuno numero di gradi di libertà:
Devianza totale: S_iS_j(y_ij-y^-)², n-1 gdl
Devianza between: S_iS_j(y^-_i-y^-)², k-1 gdl
Devianza within: S_iS_j(y_ij-y^-_i)², n-k gdl
Varianza totale (MS_T): SS_T/(N-1)
Varianza tra i gruppi (MS_B): SS_B/(k-1)
Varianza entro i gruppi (MS_W): SS_W/(n-k)

Il rapporto F
Il rapporto tra le varianza MS_B/MS_W può essere usato per esaminare ipotesi sulla significatività della differenza tra la variabilità dovuta al trattamento e quella residua.
L'ipotesi nulla è quella dove le popolazioni di provenienza dei campioni hanno medie uguali sulla variabile dipendente (H₀: µ₁=µ₂...µ_k), e l'ipotesi alternativa è quella dove almeno 2 medie sono diverse.
La varianza tra i gruppi è data dalle differenze sulla variabile dipendente, tra le medie dei gruppi sottoposti a trattamenti diversi, e riflette l'effetto del trattamento sperimentale, mentre la varianza entro i gruppi è data dalle differenze sulla variabile dipendente, tra i punteggi di soggetti dello stesso gruppo, e dato che i soggetti dello stesso gruppo son soggetti allo stesso trattamento, la varianza entro i gruppi può esser spiegata solo all'errore casuale.
Se non si può rifiutare l'ipotesi nulla, F avrà valori molto bassi (vicini ad 1), quindi se è vera l'ipotesi nulla la differenza tra gli individui dentro i gruppi è equivalente alla differenza tra gli individui che compongono i diversi gruppi, quindi MS_B e MS_W possono essere considerate 2 stime parallele e indipendenti della varianza totale della popolazione.
Se si rifiuta l'ipotesi nulla, F avrà valori alti e quindi MS_B>MS_W, e questi procedimenti che valgono per le varianze vanno bene anche per le medie.

T di student e ANOVA
Se il numero dei gruppi dove si confrontan le medie è uguale a 2 (k=2), si può usare sia la t di student, sia il rapporto F per esaminare le ipotesi, infatti F=t².
Se k>2 è sconsigliato usare la t di student, mentre si consiglia di confrontare simultaneamente la differenza tra le k medie tramite l'analisi della varianza, perchè la t di student non usa tutta l'informazione disponibile e giunge a una stima meno precisa della varianza dell'errore.

Assunzioni
Perchè si possa fare l'ANOVA:

• Gli errori (e_ij) devono seguire la distribuzione normale ed avere media = 0
• La varianza degli errori (s_e) deve essere uguale in ogni gruppo (condizione di omoschedasticità, che può essere valutata con il test di Levene).
• Gli errori (e_ij) devono essere indipendenti, cioè il punteggio di un soggetto non deve essere correlato con quello di altri soggetti, perchè la non indipendenza può avere effetti notevoli sul livello di significatività e sulla potenza del test.
  L'indipendenza viene valutata con il coefficiente di correlazione interclasse.
• Gli effetti hanno una natura additiva: ovvero la variabile sperimentale aggiunge qualcosa alla condizione di partenza e lo fa in maniera identica per tutti i soggetti, mentre la non additività aumenta debolmente l'errore sperimentale e diminuisce la potenza del test (errore però solitamente trascurabile).

Confronti tra le medie dei gruppi
Quando nell'ANOVA si ha un effetto significativo della variabile indipendente (F significativo), si può dire che c'è una differenza significativa tra almeno 2 delle medie dei gruppi confrontati, ma non si sa quali sono.
Esistono quindi 2 metodi di confronto tra medie:

1. Confronti post hoc: metodo usato quando non si sa selezionare nulla in anticipo, dove ogni media viene confrontata con tutte le altre.
   Lo svantaggio di questo metodo è che all'aumentare dei gruppi aumenta il numero di confronti ed aumenta la possibilità di commettere l'errore di primo tipo a, ovvero di rifiutare l'ipotesi nulla quando è vera.
   La disuguaglianza di Bonferroni si ha quando in un set di k confronti, il livello di probabilità che almeno uno di essi risulti significativo è <=ka, e questo vuol dire che effettuando k confronti il livello nominale di a stabilito a priori corrisponde ad un livello di ka, e quindi per risolvere questo problema si sceglie un valore a minore di .05, solitamente .05/k.
   Esistono diversi test che consentono di effettuare confronti tra tutte le possibili coppie di medie, come il Tukey HSD, il Duncan, il Dunnett.
2. Confronti pianificati: un altro metodo per diminiure la probabilità di commettere l'errore di primo tipo consiste nell'effettuare solo i confronti che sembrano più rilevanti ai fini dell'ipotesi di ricerca, quindi si decide in anticipo quali medie vanno confrontate.
   Si può quindi esaminare la differenza tra 2 medie, e queste possono essere relative a singoli gruppi o combinare insieme quelle di più gruppi.
   I confronti possono essere fatti dopo l'ANOVA nel caso in cui F risulti significativo, e per effettuare questi confronti si deve attribuire ad ogni media un coefficiente con un segno positivo o negativo.
   Le medie con un segno diverso vengono contrastate tra loro, quelle con segno uguale vengono combinate, e quelle con coefficiente 0 vengono tolte dal confronto.
   La somma dei coefficienti deve essere uguale a 0, e se anche la somma dei prodotti tra i coefficienti di un set di confronti è uguale a 0, allora si dice che i confronti sono tra loro ortogonali.
   Se 2 confronti sono ortogonali, essi danno informazioni indipendenti, ovvero il risultato del primo non permette di ottenere informazioni sul possibile esito del secondo, e viceversa, inoltre, il numero massimo di confronti ortogonali effettuabili è uguale a k-1.

Tukey least significant difference LSD (Minima differenza significativa)
Si calcola la differenza tra 2 medie, e questa differenza, per essere statisticamente significativa, deve essere maggiore in valore assoluto di t_c*s_d1:
|m_i-m_j|>t_c*s_d1
Dove tc è il valore critico della t di student ad un certo livello di probabilità e:



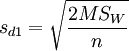
Dove n è il numero di soggetti nelle celle, e se le celle non contengono lo stesso numero di soggetti, n=(2*n₁*n₂)/(n₁+n₂).
Si consiglia inoltre di scegliere un livello critico di t pari a α/k, dove k è il numero di confronti effettuati.

Tukey honestly significant difference HSD
Si calcola la differenza tra 2 medie, e questa per essere statisticamente significativa deve essere maggiore in valore assoluto a q_{α k n-k}*s_d2, dove q_{α k n-k} (studentized range statistic) ha valori tabulari per un livello di probabilità α, per un numero di gruppi k e per un numero complessivo di soggetti N, e:

<< Lezione precedente - Prossima lezione >>

Torna all'elenco delle lezioni