Scomposizione degli effetti, soppressione, ridondanza
L'effetto non analizzato dovuto a cause correlate (ennyx1) è uguale al prodotto dei coefficienti relativi ai diversi percorsi che legano le 2 variabili.
La somma dell'effetto diretto e della componente non analizzata rappresenta l'effetto relazione totale che lega X1 a Y ed è uguale alla correlazione di ordine zero tra X1 e Y.
Quindi: effetto totale=ryx1=effetto diretto (dyx1)+effetto non analizzato(ennyx1)= β^y12+β^y21*rx1x2
E anche la correlazione tra Y e X2 è uguale alla somma dell'influenza diretta di X2 su Y(dyx2) e dell'effetto non analizzato di X2 su Y attraverso X1 (ennyx2), cioè:
ryx2=dyx2+ennyx2=β^y21+β^y12*rx1x2
La sopprensione si ha quando l'effetto non analizzato agisce nella direzione opposta a quello diretto.
La ridondanza si ha quando l'effetto diretto e quello non analizzato agiscono nella stessa direzione.
La ridondanza totale si ha quando l'effetto non analizzato assorbe completamente quello diretto.
Nella ridondanza in generale, i coefficienti di correlazione semiparziale (sr), parziale (pr) e di regressione standardizzato (β^) sono inferiori (in valore assoluto) al coefficiente di correlazione semplice r e hanno il suo stesso segno.
La sopprensione invece riguarda il caso in cui i coefficienti sr, pr e β^ sono maggiori (in valore assoluto) di r.
Se le variabili indipendenti non sono correlate viene ovviamente meno la componente relativa all'effetto non analizzato.
Differenze tra i coefficienti di regressione
Spesso il ricercatore confronta i risultati ottenuti considerando uno
stesso modello di regressione però esaminato su campioni diversi, in tal
caso deve confrontare se i coefficienti di regressione ottenuti su
diversi campioni possono essere considerati uguali.
Questo confronto può essere effettuato sia considerando i coefficienti
standardizzati che i non, dove i non standardizzati sono preferibili
perchè mantengono l'informazione relativa alla varianza delle variabili
nei diversi campioni.
La formula per confrontare i coefficienti non standardizzati è la seguente:

Il confronto tra 2 coefficienti (non standardizzati) di regressione
nello stesso campione può essere fatto solo se le variabili sono
espresse nella stessa unità di misura, mentre i coefficienti
standardizzati possono essere usati sempre, indipendentemente dall'unità
di misura in cui sono espresse le variabili.
Il confronto tra coefficienti non standardizzati avviene tramite una formula che usa la t di student:

Dove l'errore standard al denominatore può esser calcolato così:
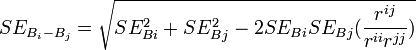
Mentre nel caso di coefficienti standardizzati, l'errore standard della differenza si calcola:

Indici diagnostici per l'analisi dei casi outlier e influential
Gli indici diagnostici sono quegli indici che consentono di diagnosticare la presenza di soggetti con un comportamento anomalo (fenomeno outlier) e/o influenzano in modo anomalo i risultati dell'analisi di regressione (fenomeno influential data point).
Esistono 3 indici in particolare:
- Distanza di Mahalanobis: è la misura della distanza del caso specifico dalla media di tutti i casi sulle variabili considerate, dove si considerano possibili outlier quelli il cui valore di distanza ha una probabilità di <.001, probabilità interpretata facendo riferimento alla distribuzione di X2 con gradi di libertà uguali al numero complessivo di variabili (dipendente ed indipendenti).
- Distanza di Cook: è una misura di quanto i residui di tutti i casi cambierebbero se un caso fosse escluso dal calcolo dei coefficienti di regressione, dove un coefficiente elevato che si distacca molto dagli altri valori indica che con l'esclusione i risultati varierebbero di molto.
- Valori di influenza (leverage): sono una misura dell'influenza di un caso sulla bontà dell'adattamento del modello di regressione, dove valori di influenza inferiori a .2 identificano casi che non sono outlier multivariati, valori tra .2 e .5 sono casi sospetti, mentre valori maggiori di .5 sono probabilmente outlier multivariati.
Regressione con variabili dummy
La variabile dummy è quella variabile di tipo dicotomica con valori 0 o 1 che serve per rappresentare le categorie di una variabile nominale.
Se la variabile ha k categorie, servono k-1 variabili dummy per rappresentare tutte le categorie della variabile.
Ad esempio se ho le 3 categorie, "sopra", "sotto", "in mezzo", posso assegnare a "sopra" 1 e a "sotto" 0, quindi il vettore (1,0) vorrà dire "sopra", il vettore (0,1) vorrà dire "sotto", il vettore (0,0) vorrà dire "in mezzo" (è indifferente quale categoria rimane esclusa dalla codifica dummy).
Le variabili dummy possono essere inserite nell'equazione di regressione come predittori di variabili quantitative, se ad esempio una variabile Y regredisce su una variabile dummy D e su una continua X, l'equazione è: Y=a+b1D+b2X+e
Dove se D=0 allora Y=a+b2X+e , se D=1 allora Y=(a+b1)+b2X+e
Queste equazioni vanno dunque interpretate come i valori attesi di Y per ogni valore che D può assumere.
Numerosità del campione e rapporto variabili/soggetti
Il requisito minimo della regressione standard e gerarchica è che il numero dei soggetti sia almeno 5 volte superiore del numero di variabili indipendenti considerate.
Si deve aumentare questo numero se la variabile dipendente ha una distribuzione asimmetrica, o se le variabili sono misurate con una forte componente d'errore (bassa attendibilità).
Nella regressione statistica invece, è consigliabile un rapporto di 40 soggetti per ogni variabile indipendente.
Considerazioni conclusive sulla regressione
Un forte limite della regressione è che non si può considerare simultaneamente più di una variabile dipendente alla volta nello stesso modello, inoltre, per parlare in maniera appropriata di nessi causali è necessario che:
- La causa di un evento deve essere sempre presente in tutte le situazioni in cui si presenta l'evento, e deve precederlo.
- Se la causa non è presente, l'evento non sussiste.
- Al variare della causa varia anche il valore dell'evento,
inoltre non bisogna trascurare fattori che possono determinare sia causa
sia effetto.
La semplice covariazione (o correlazione) di 2 elementi non prova mai l'esistenza di una relazione causale, quindi l'interpretazione va sempre effettuata con prudenza, ed è inappropriata quando i dati sono cross-sectional (quando VD e le VI sono rilevate nello stesso momento) o quando non son stati considerati tutti i fattori che possono influenzare la VD.
Piaciuto l'articolo? Lascia un commento!
EmoticonEmoticon