Psicometria (2/27): La regressione bivariata

L'analisi della regressione lineare semplice individua la retta che consente di prevedere i punteggi della variabile dipendente a partire da quella indipendente, si tratta quindi di individuare graficamente quella retta che interpreta meglio la nuvola di punti definita dalla distribuzione congiunta delle due variabili.

L'equazione del retta che lega Y a X: Y=α+ßX

Dove α è l'intercetta ovvero il punto in cui la retta incrocia l'asse delle ordinate (l'altezza della linea) corrisponde al valore di Y quando X=0, il coefficiente ß rappresenta invece l'inclinazione della retta di regressione di Y su X, ovvero il coefficiente angolare della retta.
La linearità della relazione implica che per ogni variazione di X si ha sempre la stessa variazione di Y, tuttavia le relazioni tra le variabili non sono perfette perché esse sono spesso misurate con errori o perché sono stati ommessi alcuni importanti predittori.

L'equazione della retta con l'errore: Y=α+ßX+ε

Dove la prima parte senza l'errore (detta Y') rappresenta il valore teorico di Y, ovvero il valore che si ottiene con l'equazione di regressione.
Solo se tutti i valori di Y sono sulla retta di regressione, ovvero se ε=0 è possibile individuare esattamente valori di α e ß, si dovrà quindi stimare i valori dei parametri della popolazione α e ß tramite i dati osservati su un campione in modo che si possa identificare la retta che meglio si adatta ai punti che descrivono la distribuzione delle Y sulle X.
Un metodo per stimare questi coefficienti è quello dei minimi quadrati ordinari, un metodo che rende minimo l'errore che si commette quando Y viene stimato dall'equazione di regressione.
Il metodo dei minimi quadrati ordinari identifica quella retta che riduce al minimo l'errore che viene commesso nello stimare Y da X.

L'equazione di questo metodo: e=Y-(a+bX)

L'equazione di questa retta può essere risolta tramite il calcolo differenziale, che consente di ottenere le formule di a e di b:





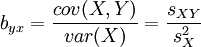
Il coefficiente a rappresenta il valore atteso di Y quando X=0, il coefficiente b rappresenta il cambiamento atteso in Y associato ad un cambiamento di un'unità in X.
Per esprimere questa relazione in una scala di minisura comprensiva bisogna standardizzare il coefficiente di regressione.
Il coefficiente di regressione standardizzato si ottiene moltiplicando il coefficiente non standardizzato per il rapporto delle deviazioni standard della VI e della VD:



Nella regressione semplice il coefficiente di regressione standardizzato è uguale al coefficiente di correlazione semplice:



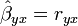
Il coefficiente di correlazione al quadrato r² è uguale al rapporto tra la varianza di Y spiegata dalla regressione con i minimi quadrati e la varianza totale di Y, ed è un indice della proporzione della varianza totale di Y che viene spiegata dalla regressione lineare di Y su X, e viene detto coefficiente di determinazione:



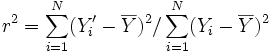
Il coefficiente di alienazione (1-r²) indica invece la proporzione della varianza totale di Y non spiegata dalla variabile indipendente, e rappresenta quindi la parte di variabilità di Y che rimane una volta che viene rimossa la parte di Y associata a X:



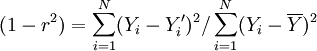
La deviazione standard degli errori (errore standard della stima) è un indice della precisione della retta di regressione.



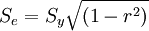
Dove se r=1, l'errore è uguale a zero.
Una stima di questo coefficiente sui dati campionati si può avere con questa formula:

<< Lezione precedente - Prossima lezione >>

 

Torna all'elenco delle lezioni