Psicometria (5/27): Adeguatezza equazione regressione multipla

L'associazione tra una variabile dipendente ed un insieme di variabili indipendenti può essere riassunta tramite coefficiente di correlazione multiplo (R), il cui quadrato viene detto coefficiente di determinazione multiplo (R²) ed indica la proporzione di varianza della variabile dipendente spiegata dalle variabili indipendenti prese nel loro complesso.

Nel caso di 2 variabili indipendenti la formula è:



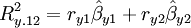
Ovvero si ottiene con la somma dei prodotti delle correlazioni semplici r e dei coefficienti β^ tra la variabile dipendente e ogni variabile indipendente.

Il coefficiente di determinazione multiplo corretto rappresenta una stima del coefficiente multiplo della popolazione, senza errore di approssimazione dovuto al numero di predittori considerati e si ottiene con la formula:
AR²=R²-(1-R²)*[k/(N-k-1)]
Dove k rappresenta il numero di predittori e N il numero di soggetti.

Il coefficiente di correlazione multiplo (R) si ottiene dal coefficiente di determinazione con la seguente formula:



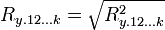
R è sempre maggiore/uguale a zero, se invece le variabili indipendenti hanno correlazioni basse tra di loro, R tende ad essere molto più elevato del più grande dei coefficienti di correlazione di ordine zero.

<< Lezione precedente - Prossima lezione >>

 

Torna all'elenco delle lezioni