Statistica (15/19): Verifica dell'ipotesi con una variabile

Verifica dell'ipotesi con una variabile dicotomica: test binomiale

1. Prerequisiti:
   a) I casi che definiscono il campione sono stati estratti in maniera casuale e indipendentemente dalla popolazione di riferimento
   b) La variabile che stiamo osservando è di tipo nominale dicotomica
2. Si formulano le ipotesi statistiche:
   a) Definire l'ipotesi nulla H₀ mettendo la probabilità uguale ad un determinato valore a seconda del tipo di ricerca effettuata
   b) Definire l'ipotesi alternativa H₁ specificando se si tratta di un'ipotesi monodirezionale o bidirezionale.
3. Fissare il livello di significatività α
4. Utilizzare il test statistico binomiale per associare una probabilità al dato campionario:
   p(k)=_nC_kp^kq^n-k
5. Prendere una decisione confrontando il p calcolato con α a seconda se:
   se p>α -> Accetto H₀
   Se p<=α -> Rifiuto H₀ e accetto H₁

Verifica delle ipotesi con una variabile metrica: test z della media

1. Prerequisiti:
   a) I casi che definiscono il campione sono stati estratti in maniera casuale e indipendentemente dalla popolazione di riferimento
   b) La variabile in esame è su scala metrica
   c) Si conoscono i parametri della popolazione, e questa ha una distribuzione normale o il campione ha un n>=30
2. Formulare le ipotesi statistiche:
   a) si definisce l'ipotesi nulla H₀ con l'uguaglianza tra il parametro della popolazione a cui il campione appartiene rispetto alla quale viene confrontato.
   b) si definisce l'ipotesi alternativa H₁ formulando l'ipotesi monodirezionale o bidirezionale.
3. Fissare il livello di significatività α
4. Identificare sulla tavola 1b i valori critici di z in base al tipo di ipotesi alternativa e al livello di α:
   a) Se l'ipotesi alternativa è bidirezionale la regione di rifiuto verrà equamente divisa tra le 2 code della curva di gauss, dividendo il livello di significatività a metà, e cercando quindi sulla tabella il valore corrispondente all'area definita da α/2.
   Verrà quindi riportato il valore con entrambi i segni z_critico=+-valore
   b) Se l'ipotesi alternativa è monodirezionale la regione di rifiuto verrà collocata su un'unica coda, definita con il livello di significatività.
   Si troverà quindi il valore critico sulla tavola 1b della distribuzione normale corrispondente ad α e nel caso l'ipotesi sia monodirezionale sinistra, il valore identificato avrà il segno negativo z_critico=-valore, in caso sia nonodirezionale destra z_critico=+valore
5. Si applica il test statistico z, dove se:
   a) conosciamo entrambi i parametri della popolazione:
   
   Dove:
   µ=media della popolazione
   σ=deviazione standard della popolazione
   M=media del campione
   n=ampiezza del campione
   b) Se non conosciamo σ:
   
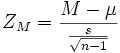
   Dove s=deviazione standard del campione
6. Prendere la decisione in base ai seguenti criteri:
   |Z| < |Z_critico| -> p>α -> Accetti H₀
   |Z| >= |Z_critico| -> p<=α -> Rifiuto H₀
   Dove |Z| vuol dire che è in valore assoluto (senza segno).

Verifica delle ipotesi con una variabile metrica: test t di student sulla media

La distribuzione t di student possiede le stesse caratteristiche della distribuzione normale ma ha una forma più schiacciata che esprime maggiore variabilità rispetto alla media.
Tanto più i campioni sono piccoli e tanto maggiore sarà la variabilità e tanto più la curva risulterà schiacciata, inoltre, tanto è minore l'ampiezza del campione tanto più aumenta il valore critico di t.
Anche in questo caso si farà riferimento ad una tabella (2) e in più saranno presenti dei gradi di libertà (gdl) che sono il numero di valori liberi di variare poste certe restrizioni.

Come condurre la verifica delle ipotesi con il test t della media

1. Prerequisiti:
   a) I casi che definiscono il campione sono stati estratti in maniera casuale e indipendentemente dalla popolazione di riferimento
   b) La variabile in esame è su scala metrica
   c) Il campione ha n<30 e/o la popolazione ha una deviazione standard non nota
2. Formulare le ipotesi statistiche:
   a) si definisce l'ipotesi nulla H₀ con l'uguaglianza tra il parametro della popolazione a cui il campione appartiene rispetto alla quale viene confrontato.
   b) si definisce l'ipotesi alternativa H₁ formulando l'ipotesi monodirezionale o bidirezionale.
3. Fissare il livello di significatività α
4. Trovare sulla tabella 2 i valori critici di t in relazione al tipo di ipotesi alternativa, il livello di α, i gradi di libertà calcolati in base all'ampiezza campionaria n, ovvero:
   gdl=n-1
5. Applicare il test statistico t di student, dove:
   a) Se conosciamo entrambi i parametri della popolazione:
   
   b) Se non conosciamo σ:
   
6. Si prende la decisione in base ai seguenti risultati:
   |t| < |t_critico| -> p>α -> Accetti H₀
   |t| >= |t_critico| -> p<=α -> Rifiuto H₀

Verifica dell'ipotesi e stima intervallare della media di una popolazione

Con la statistica inferenziale si può stabilire in termini probabilistici se un determinato campione appartiene ad una popolazione che ha quello stesso parametro.
Tramite la stima intervallare possiamo poi definire una gamma di valori entro la quale ricade il parametro in esame.
Se l'ampiezza è maggiore di 30 possiamo stabilire un intervallo di fiducia in relazione alla media della distribuzione normale con questa formula:



Se le ampiezze dei campioni sono minore di 30 possiamo stabilire l'intervallo di fiducia con la seguente formula:



Calcolando l'intervallo di fiducia si parte dalla media campionaria per identificare un intervallo di valori entro il quale molto probabilmente ricade il parametro in esame.

<< Lezione precedente - Prossima lezione >>

 

Torna all'elenco delle lezioni