Le misure di variabilità servono per capire come vengono distribuiti i dati intorno agli indici di tendenza centrale.
Ci sono diverse misure di variabilità:
Campo di variazione (range)
Il range è la quantificazione dei valori della variabile compresi tra il minimo e il massimo.
Per esempio, su una scala a punteggio da 1 a 20, il valore minimo totalizzato può esser stato 3 ed il massimo 15.
Questo indice di variabilità ha il limite ovvio che vengone presi in considerazione solo gli estremi, non considerando valori intermedi e frequenze.
Differenza interquartile
Si divide la distribuzione in 4 parti utilizzando 3 valori detti quartili.
Il primo quartile Q1 rappresenta il primo 25%, il secondo quartile Q2 il 50% dei casi, ed il 75% al di sotto del terzo quartile Q3.
La differenza interquartile è la differenza tra il terzo quartile ed il primo.
DI = Q3 - Q1
Questo indice prende in considerazione solo la parte centrale della distribuzione che equivale al 50% dei valori presenti.
Misure di deviazione dalla media
Per calcolare la variabilità della distribuzione si calcola la deviazione (o scarto) di ciascun valore dalla media e se ne trova il valore medio.
La somma di tutti gli scarti dalla media risulta sempre uguale a zero.
Per calcolare questa variabilità si può procedere in 3 modi:
1) Scostamento semplice medio (SSM)
Si ottiene sommando tutti gli scarti dalla media in valore assoluto e dividendo il risultato per il numero di valori/osservazioni.
Il valore ottenuto esprime quanto in media i valori discostano dal valore medio della distribuzione.
Esempio: n=4; M=5
| Valore | Calcolo | Valore assoluto |
| 3 | 3-5 | 2 |
| 4 | 4-5 | 1 |
| 5 | 5-5 | 0 |
| 8 | 8-5 | 3 |
| ∑= 6 |
SSM = [∑(xi-M)]/n = 6/4 = 1.5
2) Varianza e deviazione standard
La varianza si ottiene sommando gli scarti della media, dividendoli per il numero totale delle osservazioni (dei valori, ovvero di n).
La varianza è un indice di variabilità ed è sempre positivo.
Elevando i valori al quadrato, però si cambia unità di misura e quindi si hanno problemi quando bisogna fare dei confronti (es diventano da cm a cm2), quindi per ovviare a questo problema, si fa la radice quadrata della varianza, ottendendo così la deviazione standard.
La deviazione standard (o scarto quadratico medio) è un valore sempre positivo che indica quanto mediamente i dati osservati discostano dalla media.
Nella popolazione la deviazione standard si indica con il simbolo greco sigma σ , mentre la varianza con sigma al quadrato σ2.
Nel campione invece si utilizzano semplicemente le lettere s e s2.
Nel caso i valori non siano a frequenza unitaria, occorre come al solito moltiplicare ciascuno scarto al quadrato per la relativa frequenza.
| Varianza nella popolazione | Varianza nel campione |
| Frequenza unitaria | Frequenza unitaria |
 |
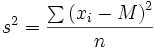 |
| Frequenza non unitaria | Frequenza non unitaria |
 |
 |
| Deviazione standard nella popolazione | Deviazione standard nel campione |
| Frequenza unitaria | Frequenza unitaria |
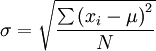 |
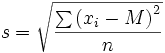 |
| Frequenza non unitaria | Frequenza non unitaria |
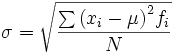 |
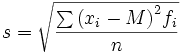 |
Dove:
µ: media della popolazione
M: media del campione
xi: valore
fi: frequenza di ciascun valore
N: numero dei casi della popolazione
n: numero dei casi del campione
Calcolare la varianza e la deviazione standard in questo modo può risultare molto lungo se ci sono tanti valor, ecco una formula generica che semplifica i calcoli:
| Varianza nella popolazione | Varianza nel campione |
| Frequenza unitaria | Frequenza unitaria |
 |
 |
| Frequenza non unitaria | Frequenza non unitaria |
 |
 |
| Deviazione standard nella popolazione | Deviazione standard nel campione |
| Frequenza unitaria | Frequenza unitaria |
 |
 |
| Frequenza non unitaria | Frequenza non unitaria |
 |
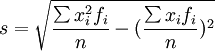 |
Questi indici vengono riportati nei seguenti modi, a seconda che si esamini un campione o la popolazione: M±s o M±σ
3) Coefficiente di variabilità
Consente di confrontare la variabilità di due o più distribuzioni e si calcola dividendo la deviazione standard per la media.
Questa è una variabilità relativa, ed il valore ottenuto è espresso in percentuale:
V = (s/M)*100 o V = (σ/µ)*100
Grazie al coefficiente di variabilità è possibile fare contronti tra distribuzioni in termini di variabilità assoluta e relativa, indipendentemente dall'unità di misura della
variabile.
Scale di misura e indici di variabilità
Questi indici di variabilità possono essere utilizzati quando si lavora su scale di misura di tipo quantitativo, su scale ad intervalli e a rapporti.
Piaciuto l'articolo? Lascia un commento!
EmoticonEmoticon