Le misure di tendenza centrale sono quei valori che indicano il centro della distribuzione dei dati.
Si dividono in 3 categorie: media, mediana e moda.
Media
La media è il valore centrale di un insieme di dati.
La media si calcola sommando tutti i valori presenti nella popolazione o nel campione in esame e dividendoli per l'ampiezza N della popolazione o n del campione.
Se si tratta di valori con frequenza non unitaria è necessario moltiplicare ogni valore per la rispettiva frequenza e poi fare la sommatoria.
Nel caso della popolazione la media si indica con la lettera greca µ, mentre nel caso del campione si utilizza la lettera latina M.
La somma degli scarti al di sopra della media è uguale alla somma degli scarti al di sotto della media.
La media è il baricentro della distribuzione, il fulcro.
Calcolo della media
| Campione | Popolazione | ||
| Frequenza unitaria | Frequenza non unitaria | Frequenza unitaria | Frequenza non unitaria |
| M=(∑xi)/n | M=(∑xi*fi)/n | µ=(∑xi)/n | µ=(∑xi*fi)/n |
Se la variabile è ditocomica di tipo 0 e 1, la media si calcola tenendo in considerazione solo la frequenza di 1: M=f1/n
Mediana
La mediana è quel valore che divide la distribuzione di frequenza a metà.
La mediana si indica con Me o Mdn.
Per calcolare la medianadi una distribuzione, occorre ordinare i valori ordine crescente e si prende il valore centrale.
Se il numero di valori è pari, bisogna prendere i due valori centrali della distribuzione (es x4 e x5), e in caso di variabili continue, basterà calcolarne la media (es (x4+x5)/2 ),.
In caso di valori con frequenze diverse da uno, occorrerà prima calcolare le varie frequenze e le frequenze cumulate, e si applicherà quanto detto sopra, però tenendo conto dei valori centrali delle frequenze cumulate.
In caso ci si ritrovi a cavallo tra 2 frequenze cumulate, ad esempio tra 7 e 8, si prenderà la frequenza cumulata che le contiene entrambe, ovvero la successiva frequenza cumulata in ordine nella lista, per esempio 9, e per ricavarne il valore della mediana, basterà poi prendere il valore corrispondente.
La mediana è una misura la tendenza centrale e rappresenta il centro della distribuzione, e ci indica dove la distribuzione di frequenza è divisa in due parti uguali.
Calcolo della mediana frequenza unitaria
| Casi pari | Casi dispari | ||
| (n/2) <= posizione md <= (n/2)+1 | (n+1)/2 |
Moda
La moda è quel valore che ha la frequenza più elevata.
Quindi per trovare la moda basterà trovare la frequenza più elevata ed andare a vedere a quale valore appartiene.
La moda si indica con Mo o Mod, ed è unimodale se è un valore unico (ovvero se c'è un solo valore ad avere la moda più alta), bimodale quando sono 2 i valori con frequenza elevata e multimodale quando i valori a frequenza elevata sono più di 2.
In caso di frequenza unitaria o di frequenze molto simili si parla di distribuzione amodale.
Individuazione della moda (in giallo)
| Valore | Frequenza |
| 1 | 4 |
| 2 | 3 |
| 3 | 6 |
| 4 | 8 |
| 5 | 1 |
La media è utile per conoscere l'andamento generale di un'insieme di dati, ma è molto sensibile ai valori eccessivamente alti o bassi, che possono influenzarne notevolemente il calcolo, in tal caso può essere utile calcolare mediana per conoscere l'indice di tendenza centrale.
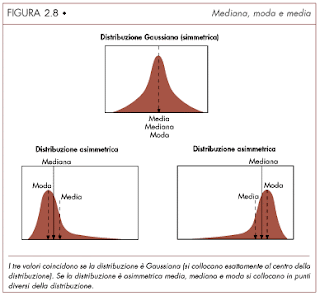
Si ha una distribuzione simmetrica quando i valori sono equamente distribuiti a destra e a sinistra della media, che coincide quindi con la moda e la mediana.
La distribuzione è asimmetrica negativa, quando la media è inferiore della mediana e la mediana è inferiore della moda.
Mentre è asimmetrica positiva, se la media è maggiore della mediana e questa è maggiore della moda (detto valore modale).
Gli indici di tendenza centrale possono essere utilizzati per qualsiasi tipo di scala ad intervalli e a rapporti.
Per variabili misurate su scale ordinali, non è possibile calcolare la media, mentre la moda e la mediana si.
Infine, per variabili nominali non ha senso calcolare media e mediana, ma la moda si.
Piaciuto l'articolo? Lascia un commento!
EmoticonEmoticon