Una distribuzione di probabilità è data dall'insieme delle probabilità associate ai possibili risultati di un esperimento.
Le distribuzioni teoriche non sono frutto di dati realmente raccolti, ma sono dati ricavati da delle teorie matematiche.
Distribuzione binomiale
I dati binomiali sono i risultati della misurazione di una variabile dicotomica, ovvero una variabile che consente solo 2 tipi di valori (giusto/sbagliato, vero/falso, maschio/femmina ecc...).
Si può prendere un singolo evento oppure un insieme di eventi binomiali e costruire la distribuzione di probabilità binomiale.
Per costruire la distribuzione di probabilità binomiale occorre
conoscere la probabilità di successo (p) per ogni singolo evento, il
loro numero complessivo (n) e calcolare la probabilità facendo variare k
da 0 a n. Infatti nella distribuzione binomiale, i possibili risultati
sono dati dal numero di eventi favorevoli (k), rispetto al numero di
complessivo di eventi della distribuzione in esame.
Avendo ad esempio una sola domanda di tipo corretto o scorretto, si
avrà la risposta corretta (C) o la risposta scorretta (S), k può
assumere solo 2 valori, 0 o 1, ciascuno con la probabilità associata p
di .50 (o 50%).
Avendo invece 2 domande, si potranno avere le seguenti casistiche: entrambe corrette (CC), una sola corretta (CS o SC), entrambe scorrette (SS), e k potrà variare da 0 a 2.
Quindi:
entrambe corrette: p(C^C) = p(C)*p(C) = .50*.50 = .25
entrambe scorrette: p(S^S) = p(S)*p(S) = .50*.50 = .25
Mentre se si ha una corretta ed una scorretta, bisogna considerare entrambi incasi (CS e SC), e si calcolerà quindi la probabilità disgiunta dei 2 eventi:
p(C^S) U p(S^C) = (.50*.50)+(.50*.50) = .50
Nel caso di 3 domande, per velocizzare il calcolo si usa l'equazione che esprime la funzione di probabilità binomiale:
p(k) = nCk*pk*qn-k
n(nCk) è il coefficiente binomiale, dove C sono le combinazioni.
Le combinazioni si calcolano con i numeri fattoriali:
Esempio: 4C2 = 4!/[2!(4-2)!] = (4*3*
I numeri fattoriali si calcolano con la seguente formula:
n! = n*(n-1) * (n-1) * (n-2) * (n-3) ... (n-n+1)
es: 3!=3*(3-1)*(3-2)*(3-3+1)=6
Quando è necessario si può sviluppare il fattore fino ad un certo punto, ricavando il risulato parziale e un fattore minore, ad esempio: 4!=4*(4-1)*(4-2)*(4-3)*2!, dove ci si è fermati al 2!
Le combinazioni di n elementi presi a k a k, sono tutti i possibili raggruppamenti di k elementi entro n (con k<n) che si distinguono tra loro unicamente per la presenza di elementi diversi:
Ovvero se ad esempio si ha 3C2, vuol dire che si vuole sapere quanti gruppi si possono formare da 2 elementi con 3 elementi a disposizione, avendo tra loro almeno un elemento diverso.
Le disposizioni di n elementi presi a k a k, sono tutti i possibili raggruppamenti k elementi entro n (con k<n) che si distinguono per l'ordine e la presenza di elementi diversi:
Ovvero se ad esempio si ha 3C2, vuol dire che si vuole sapere quanti gruppi si possono formare da 2 elementi con 3 elementi a disposizione, avendo tra loro almeno un elemento diverso e ordinamento diverso (ABC, BCA).
Le permutazioni di n elementi presi a n a n, sono tutte le serie ordinate di tali elementi:
nPn=n!
Le permutazioni sono gruppi di sequenze, ovvero se in una corsa ci sono 5 cani, il risultato della permutazione darà il numero di gruppi che è possibile creare con diverse sequenza d'arrivo (es gruppo 1 cani in ordine d'arrivo: A,C,B,E,D, gruppo 2 ordine: E,D,C,B,A, ecc...).
La somma di tutte le probabilità associate ai risultati ∑p(k) è uguale a 1.
La forma della distribuzione in caso di p=q è simmetrica rispetto al valore centrale, vicino al quale sono collocate le probabilità più elevate di successo.
Con p!=q si avrà una distribuzione asimmetrica, dove se p<q si avrà una asimmetrica positiva, e con p>q una asimmetrica negativa.
Asimmetrica positiva:
La distribuzione binomiale può essere utilizzata non solo quando un soggetto è soggetto a più prove, ma anche quando più soggetti stanno svolgendo la stessa prova.
Ovvero, l'equazione binomiale definisce la probabilità di un singolo soggetto di k scelte corrette su n prove, oppure la probabilità di n soggetti che svolgono la stessa prova di compiere k scelte corrette.
In entrambi i casi si calcola la probabilità relativa al risultato k ottenuto complessivamente da un campione che può essere costituito da n soggetti o da n prove.
Media e deviazione standard della distribuzione binomiale
La media è il risultato più probabile, quello più atteso.
Se ci si trova davanti ad una sola prova, la media è uguale a p, altrimente, se le prove sono n, la media è:
µ = n*p
La deviazione standard invece:
La distribuzione continua
La distribuzione normale è una distribuzione teorica tra le più comuni, nota anche come curva a campana (o gaussiana), o anche come curva ad errori, in quanto una serie di misurazioni ripetute di errore tendono a distribuirsi normalmente.
Dove il pigreco equivale a 3.14, e equivale a 2.72.
Nella rappresentazione grafica, l'area totale al di sotto della curva (da - infinito a + infinito) è uguale a 1 e corrisponde alla probabilità totale.
Si po poi calcolare per ogni valore di x la probabilità di verificarsi, definendo l'intervallo fino al valore x, calcolato con:
L'integrale consente di calcolare la somma di aree quando le variabili sono continue.
Tutte le distribuzioni normali hanno alcune caratteristiche comuni, ad esempio:
sono simmetriche rispetto alla media, dato che i valori di x si posizionano ad una stessa distanza sopra o sotto la media.
Le aree tra - infinito e la media e + infinito e la media, sono uguali a .50, la metà dell'intera area che ricordiamo è 1.
Anno tutte la forma a campana con una maggiore concentrazione dei casi intorno alla media, ed una minore nelle code.
La curva presente alcuni punti di flesso in corrispondenza di +- una deviazione standard dalla media, in cui la curva diventa da convessa a concava.
La distribuzione assume il suo punto massimo in corrispondenza della media, che è quindi il valore più probabile con frequenza più alta.
La media coincide con la moda e con la mediana.
La distribuzione normale è detta quindi unimodale.
La curva è detta asintotica dato che le code tendono all'infinito, senza toccare mai l'ascisse.
Inoltre, qualsiasi siano i parametri, l'area della porzione di curva delimitata dalla media è un'ordinata espressa in ordine di deviazione standard costante: tra -1 e +1 deviazione standard si trovano il 68.26% dei casi, tra -2 e +2 il 95.46%, tra +3 e -3 il 99.73% dei casi.
La distribuzione normale standardizzata si ottiene trasformando i valori della variabile x in punteggi standardizzati z.
La f(z) ha µ=0 e σ=1 ed è sempre rappresentata da una sola curva, mentre la distribuzione normale non standardizzata è rappresentabile da infinite curve a seconda dei valori dei parametri µ e σ.
L'uso di questa distribuzione consente di individuare le probabilità relative ai diversi intervalli dei valori tramite le tavole di probabilità.
Per poter calcolare la proporzione di valori sottostanti la curva utilizzando le tavole di probabilità occorre trasformare i risultati grezzi in punti z, e ciò è possibile solo se i punteggi si distribuiscono normalmente.
Le tavole riportano l'area compresa tra la media e z, e l'area che si colloca oltre il punto z, nella coda della distribuzione.
Nella prima colonna della tavola si ha il valore di z con il primo decimale e nella prima riga la seconda cifra del decimale.
Visto che si tratta di una distribuzione normale, i valori di z nelle tavole sono sempre positivi.
Quando usare le tavole della distribuzione normale standardizzata
- Per determinare l'area al di sopra o al di sotto di un valore o l'area compresa tra due valori di una variabile.
- Per determinare le frequenze teoriche corrispondenti a una determinata area.
- Per determinare i valori grezzi conoscendo le aree.
Per calcolare l'area compresa tra due valori zeta, occorre distinguere il caso in cui un valore è positivo e l'altro è negativo, dal caso in cui siano entrambi positivi o entrambi negativi.
Tabella riassuntiva del calcolo delle aree della distribuzione normale con le tavole:
| Valori che definiscono l'intervallo | Segno dei valori che definiscono l'intervallo | Operazioni sulle aree identificate sulla tavola |
z1 e z2
|
entrambi positivi o entrambi negativi | Differenza: Area maggiore - Area minore |
| uno positivo ed uno negativo | Somma: Area1+Area2 |
|
z e infinito
|
entrambi positivi o entrambi negativi | Differenza: .5000-area |
| uno positivo ed uno negativo | Somma: .5000+area |
Le aree corrispondono alle frequenze relative, e conoscendo le fr, possiamo calcolare le frequenze assolute moltiplicando l'area ottenuta per il numero totale di frequenze N.
Riepilogo di come calcolare la probabilità con la distribuzione normale
1) Trasformare i valori grezzi in valori z:
2) Rappresentare graficamente la curva normale individuando i punti z e il valore medio.
3) Usare le tavole della distribuzione normale:
- Trovare il valore di zeta con la prima cifra decimale nella colonna di sinistra, individuare la seconda riga decimale nella prima riga, e ricercandone l'intersezione si ricava dalla tavola 1a l'area tra la media e z, e nella tavola 1b l'area da z al resto della coda della distribuzione.
- Per i valori di z con segno negativo si utilizza la parte positiva della distribuzione.
- Quando si calcolano le aree bisogna ricordare che la somma la somma totale dell'are al di sotto della curva è guale a 1 e la metà è .5000.
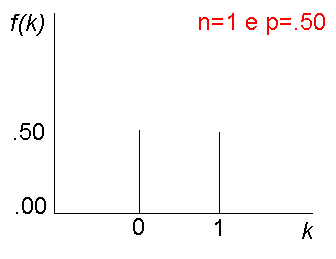

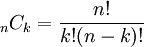
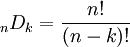


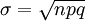

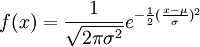
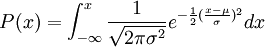
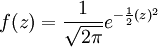
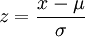
Piaciuto l'articolo? Lascia un commento!
EmoticonEmoticon